Магічні квадрати з простих чисел

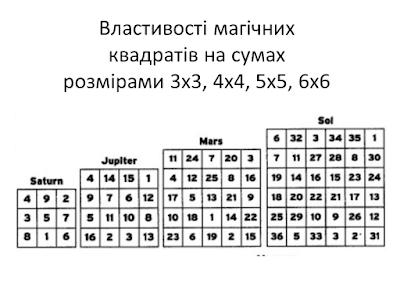
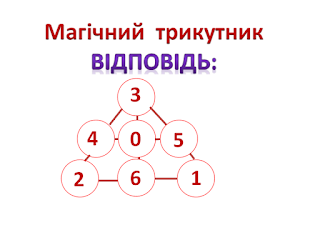
 Дослідіть властивості наступних магічних квадратів і зобразити їх у вигляді вище зазначених схем

Приклад магічних квадратів на простих числах.

Набір з дев'яти простих чисел: 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879 – приваблива не тільки тим, що вона є арифметичною прогресією з різницею 210, але і здатністю розміститися в дев'яти клітках так, що утворюється магічний квадрат з константою, рівній різниці двох простих чисел: 3119 – 2:

1669	199	1249
619	1039	1459
829	1879	409

Наступний, десятий член даної прогресії 2089 – також просте число. Якщо видалити із зграйки число 199, але включити 2089, то і в цьому складі зграйка може утворити магічний квадрат – тема для пошуку.

Слід зазначити, що існують і інші магічні квадрати, що складаються з простих чисел (див. Математика в школі № 4/95):

1847	6257	6197	3677	1307	1877	2687
2267	1427	5987	5927	1667	2027	4547
2897	947	2357	4517	3347	5867	3917
3557	4157	4397	3407	2417	2657	3257
4337	5717	3467	2297	4457	1097	2477
4817	4767	827	887	5147	5387	1997
4127	557	617	3137	5507	4937	4967

Запропонований числовий квадрат цікавий оскільки

1.     Він є магічним квадратом 7х7;

2.     Він містить в собі магічний квадрат 5х5;

3.     Магічний квадрат 5х5 містить в собі магічний квадрат 3х3;

4.     Всі ці квадрати мають одне загальне центральне число – 3407;

5.     Всі 49 чисел, що входять в квадрат 7х7, закінчуються цифрою 7;

6.     Всі 49 чисел, що входять в квадрат 7х7, - прості числа;

7.      Кожне з 49 чисел квадрату 7х7 подається як 30n + 17.